Autoencoders for Semi-Visible Jet Detection

Contents

• overview
• personal contributions
• analysis
• future work

overview

Semi-visible jets are a promising explanation for both the missing transverse momenta in proton-proton collisions at the LHC and for the nature and origin of Dark Matter. This theory admits new “dark sector” particles; however, such particles have a wide range of unconstrained parameters. Since dedicated searches across this large phase space can be impractical, we present here an unsupervised method for Semi-Visible jet detection, using neural autoencoders.

personal contributions

I recieved funding for this project from both the University of Michigan International Institute and the Swiss Office of Science. I lived in Geneva, Switzerland and worked at CERN during the Summer of 2019.

While the idea of using neural autoencoders for this analysis was sparked by conversations with Annapaola de Cosa and Maurizio Pierini, I am the sole author of all work involved in this analysis. This includes

• a ROOT C++ based data selection chain
• a high-performance Python data processing chain
• simultaneous Autoencoder training and testing frameworks, written in Python with Keras/Tensorflow
• analysis and plotting of results, again in Python

The code for this repository is given here; all code, plots, and results shown here are my work.

We plan to submit a paper on this work shortly, and this work was the subject of my (unfortunately canceled) poster presentation at the March 2020 APS meeting.

analysis

In the case we investigate for this analysis, we consider a hypothetical dark sector W-boson \(W^\prime\). For this particle, the chief unconstrained parameters are

1. the fraction of dark sector particles decaying back to the Standard Model \(r_{\text{inv}}\) and
2. the mass of the \(W^{\prime}\) boson

Rather than deploy an ensemble of searches across a grid of possible combinations - as might be done in a traditional analysis - we make use of a neural autoencoder to estimate the QCD background in an unsupervised manner. We then evaluate this autoencoder over a wide range of signal parameters, and show that the autoencoder has excellent signal discovery across a range of signal parameters.

This is done by training autoencoders on a sample of pure background data by minimizing their reconstruction error for each jet (parameterized by Mean Squared Error). We then evaluate the AEs on mixed data/signal samples, and show that they are able to easily pick out signal from data.

We represent each jet as a feature vector, comprised of 19 position, energy, and jet constituent variables. This also means that our AEs have 19 inputs/outputs, with some smaller bottleneck size. We determined the optimal bottleneck size to be 8 for this problem.

The autoencoder architecture used in this analysis is shown below:

Autoencoder architecture for this analysis

The full analysis proceeds as follows:

1. Generate \(\mathcal{O}(10\text{ million})\) QCD background events and some number of SVJ signal events using Pythia

2. Perform a generic Semi-Visible Jet analysis selection on QCD and SVJ events, requiring high transverse momentum and close jets (efficiency for QCD \(\approx\)1%), using ROOT C++

3. Traverse selected events and save relevant jet features to HDF5 format files, using Python

4. Train \(\mathcal{O}(100)\) identical neural autoencoders on the QCD dataset, and select the top 10% of those with the lowest reconstruction error (best convergence)

5. Evaluate the autoencoders on data and place cuts on their reconstruction errors at selected efficiencies (i.e. take only those jets with the highest 0.1% reconstruction error).

Following this procedure, we can analyze the efficiency at various reconstruction error cut values for one of the selected autoencoders. This is used for all analyses below.

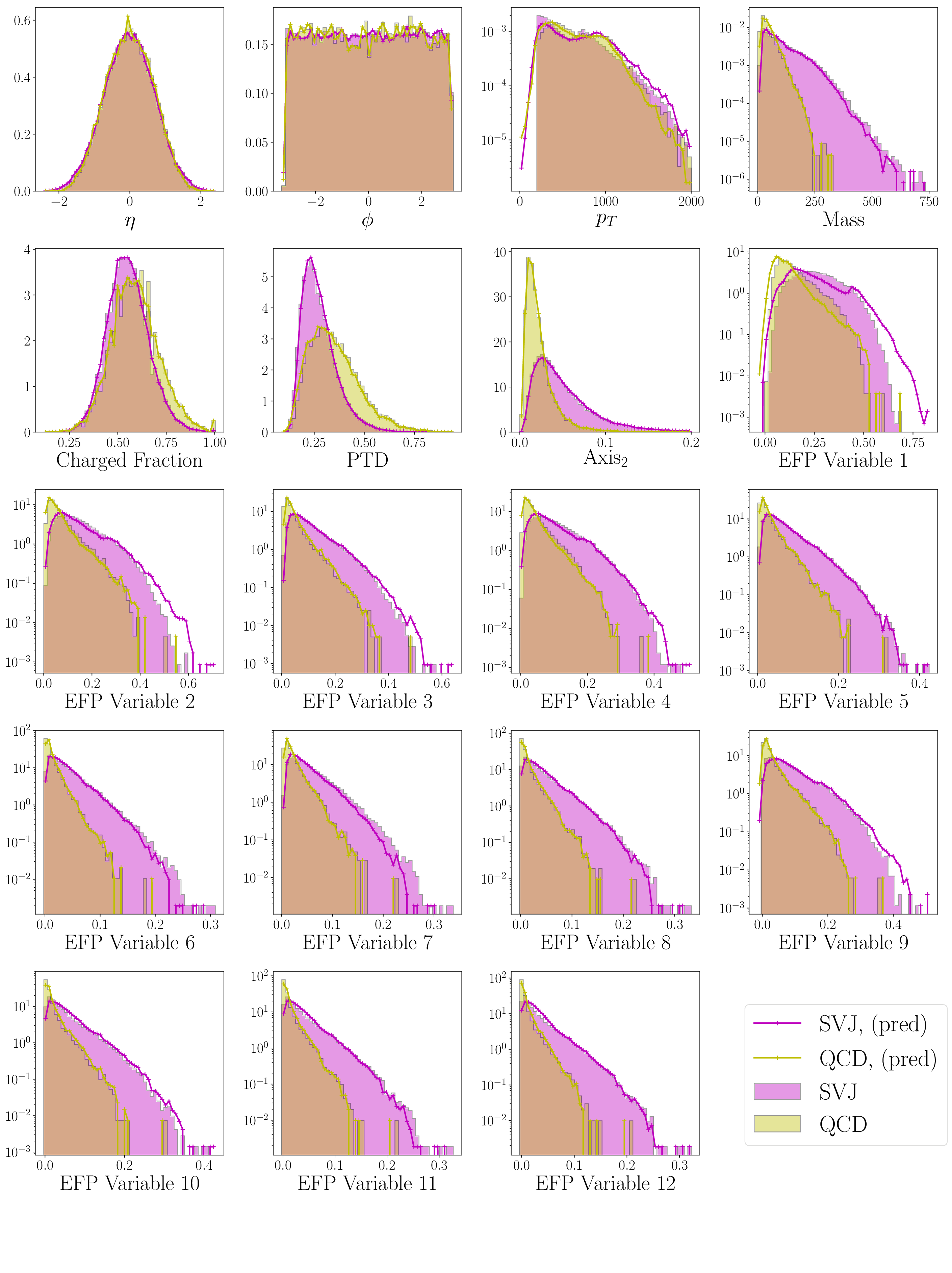
The input and reconstructions distributions of the data are shown below. These include a set of Energy Flow Polynomials, which form a basis for describing jet substructure. We see from these distributions that in general, the reconstructions of SVJ signal are worse than the reconstructions of QCD background, implying that we will see some performance increase.

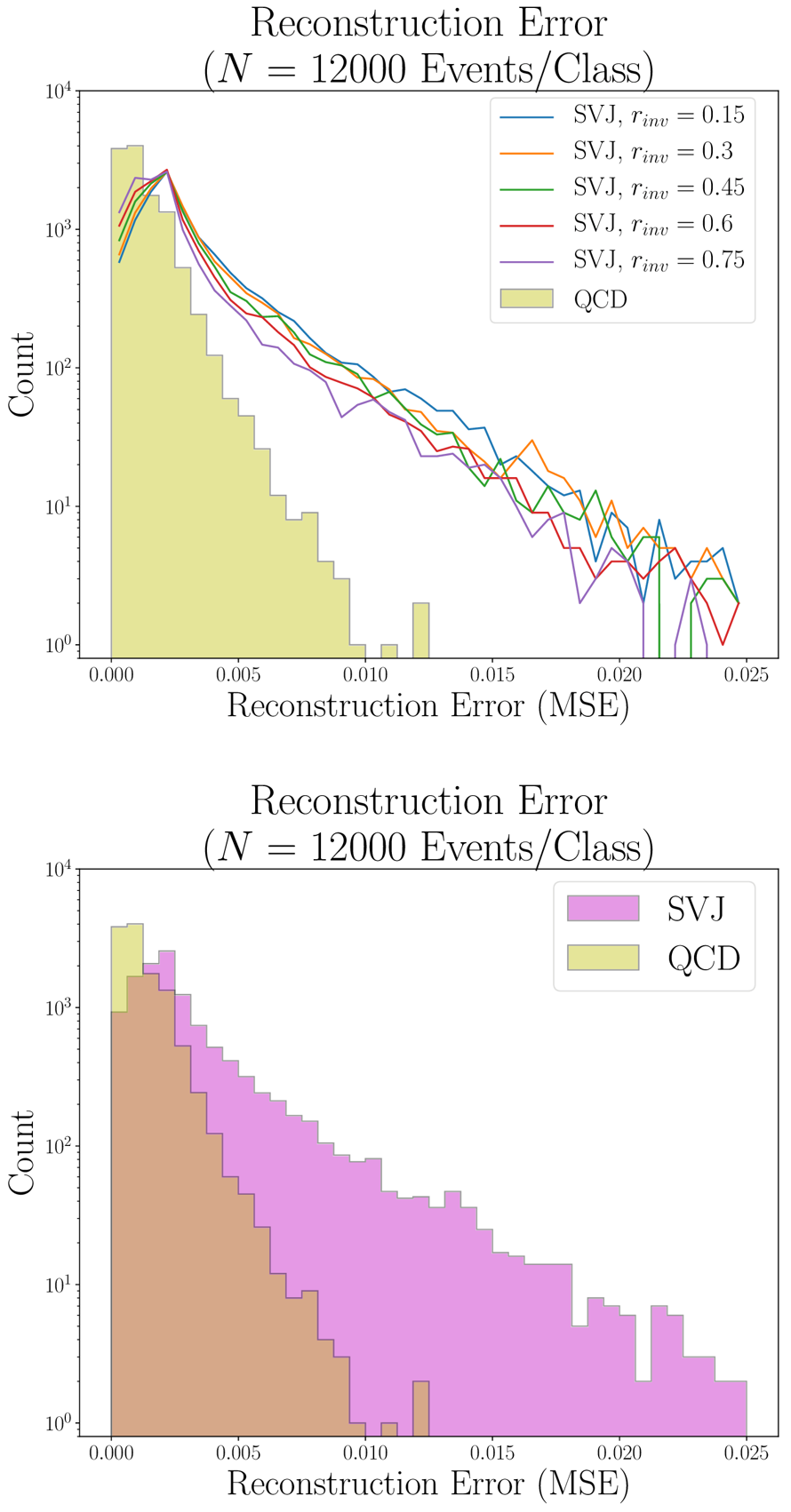
Also shown are the reconstruction error distributions, which parameterize the total error across all features. As expected, we see that these are significantly higher in general than for the SVJ than the QCD.

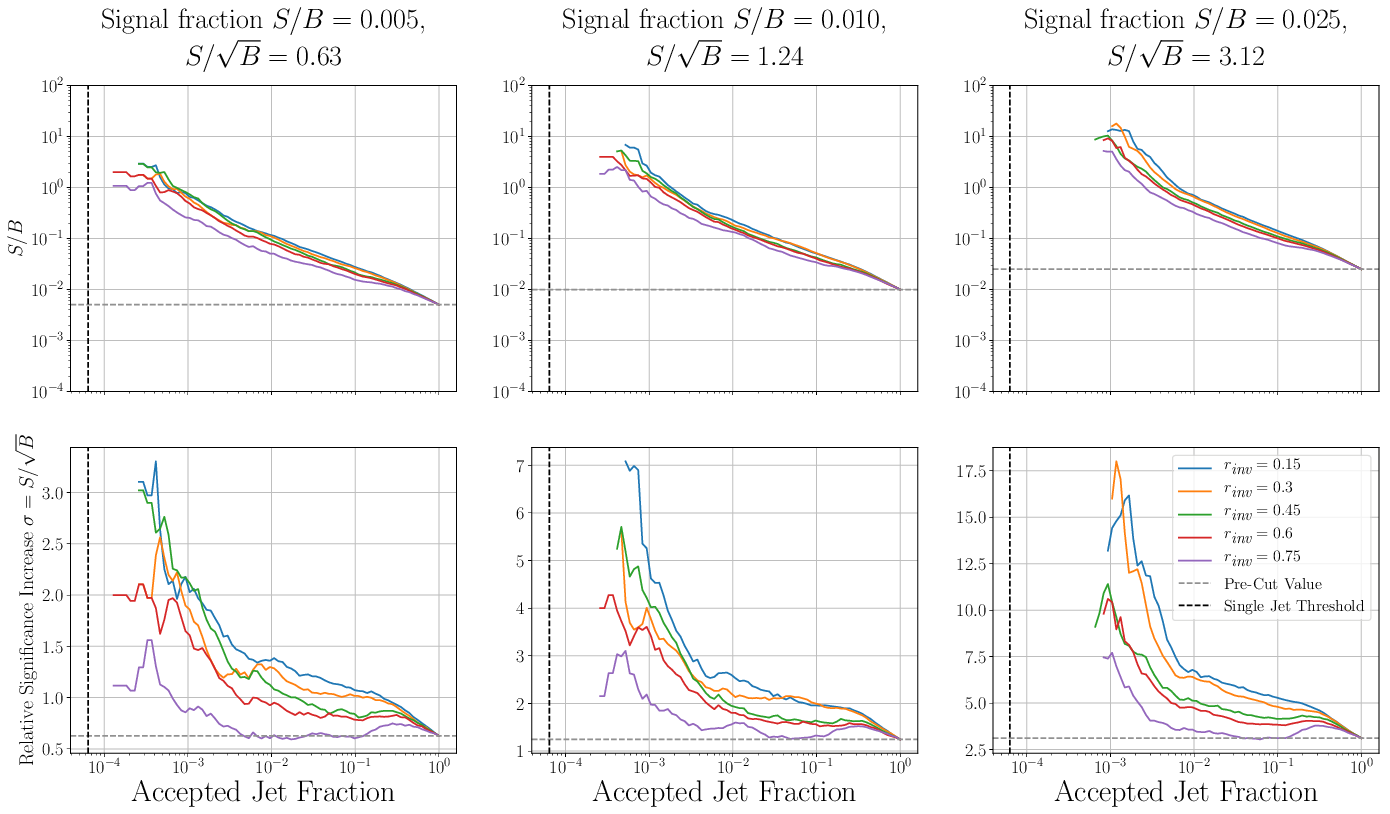
To quantify the performance over a rance of MSE cuts, we show the relative significance increases and S/B ratios across a cut on the autoencoder MSE betweeen inputs and reconstructions. By observation, significance increases are ~6 in the maximum range, indicating excellent signal discovery.

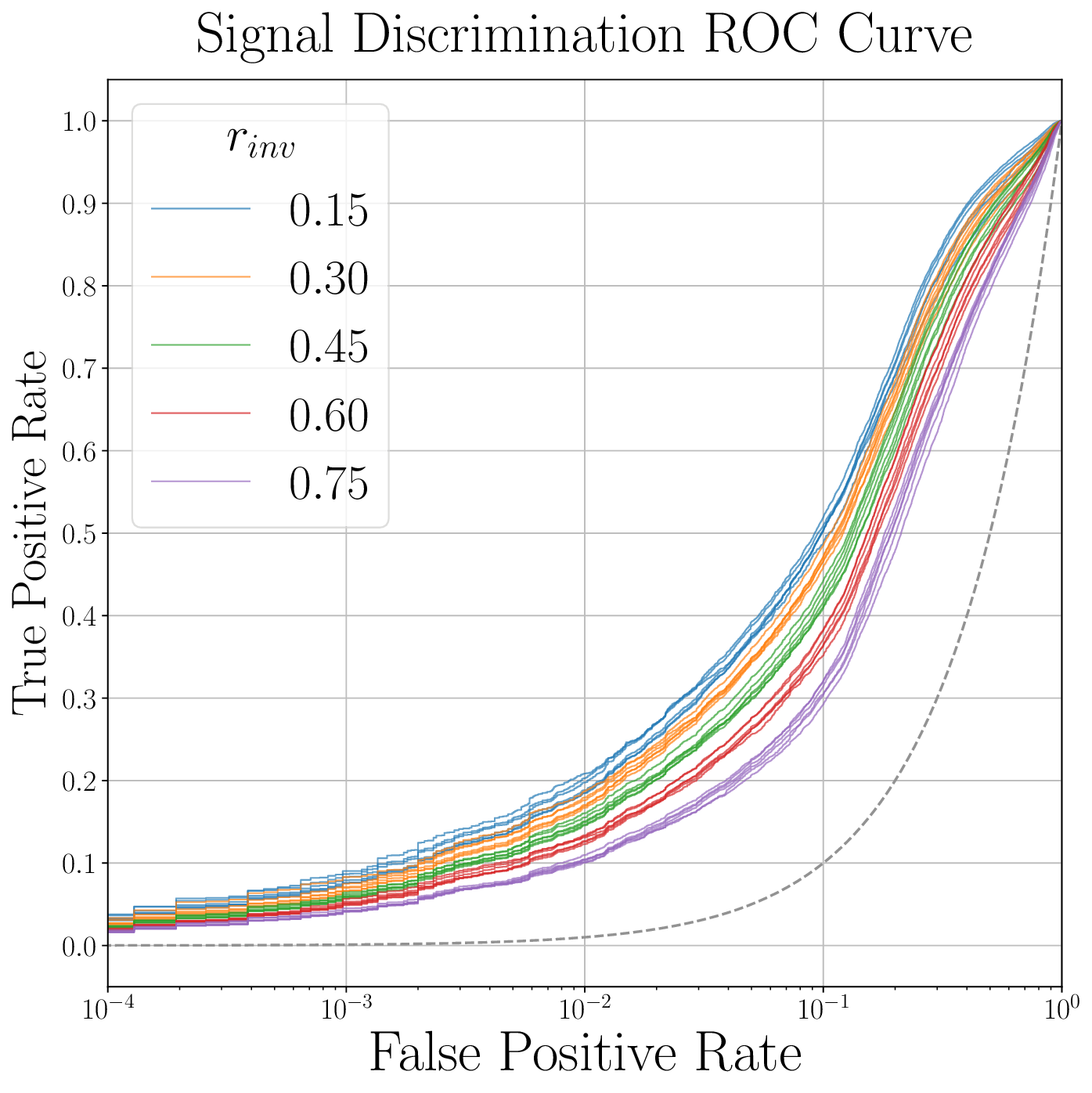
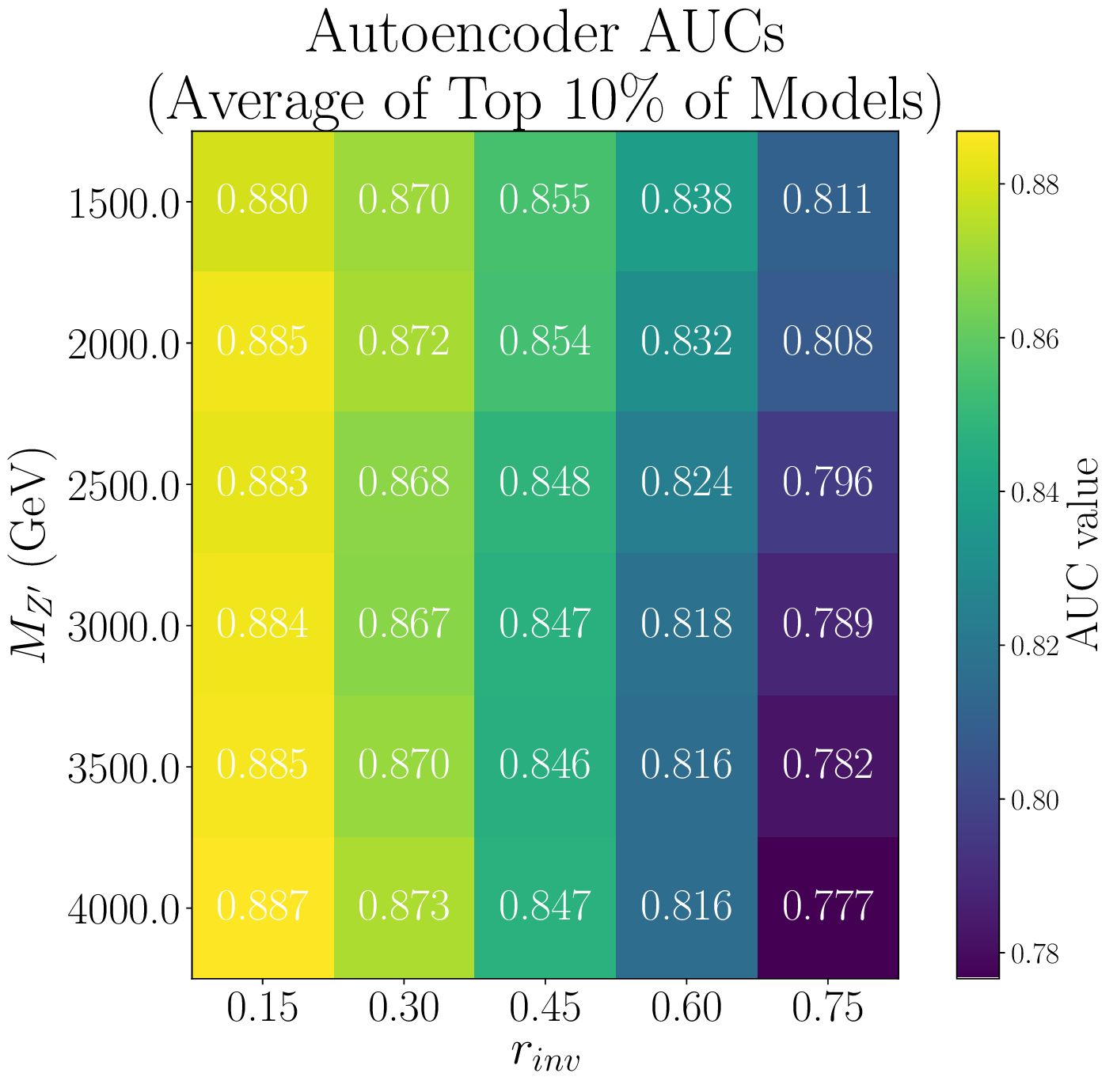
We can also examine the ROC curves and AUC scores for the average of the selected models across a range of signal models, indicating that performance is generally fairly good for all signal models. Note that in general, higher \(r_{inv}\) signals yield lower AUC scores and performances. Also note that performance generally does not become good before very low acceptance fractions.

future work

While this work has shown significant promise in detecting Semi-Visible jet signals in an unsupervised fashion, there are a few possibilities which I have a particular interest in pursuing in the future.

• Replacing autoencoders with other density estimators, such as RNADE or ANODE

• Testing how signal identification changes as signal is injected into the training sample, and after which point the AEs will learn the signal patterns

• Testing the ability of neural autoencoders to learn detector defects and other experimental quirks; this would be done by programming “defective” hardware elements into our simulations. This gives purpose to the inclusion of jet position (\(\eta\) and \(\phi\)) in the jet features.